A Scientific Danger Restrict System for A Crypto Futures Alternate

The beneath insightful new article penned by KuCoin’s founder, Michael Gan, and Head of Derivatives, Ken Tian, delves into the revolutionary backend logic of KuCoin’s new threat restrict system for cross-margin, much like conventional finance, showcasing KuCoin’s dedication to technical excellence and strong threat administration methods.

Introduction

Many cryptocurrency exchanges undertake advanced threat administration measures to forestall liquidation dangers. These embody setting multi-level threat limits and proscribing the usage of excessive leverage. Moreover, exchanges dynamically regulate parameters like threat limits and margin charges based mostly on the underlying asset’s worth and market liquidity. Nonetheless, these processes aren’t solely advanced but additionally lack clear administration requirements, requiring important assets to keep up a system that will not be internally constant—for instance, growing capital could not permit for bigger positions because of abrupt adjustments in leverage tiers.

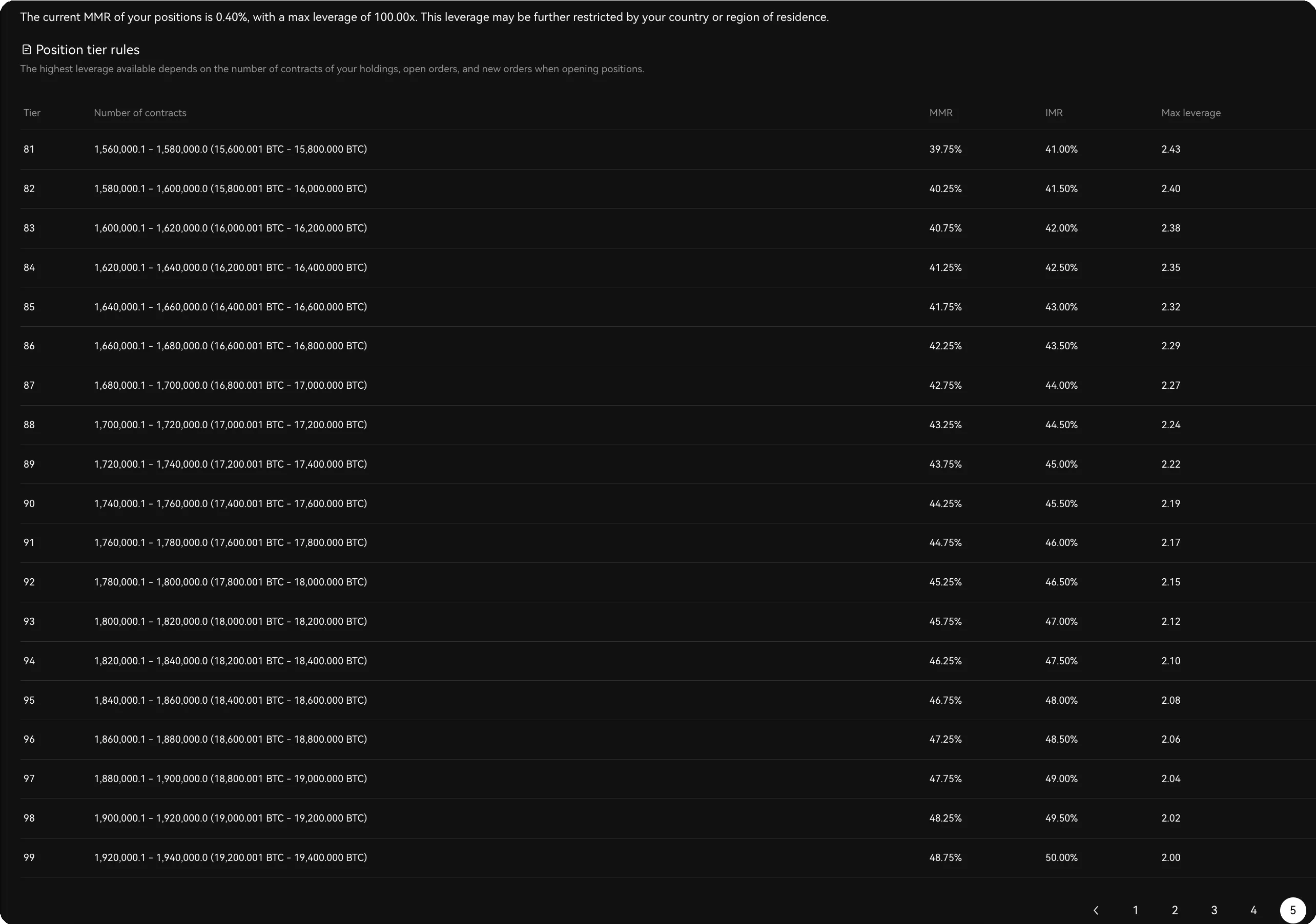
On some buying and selling platforms (see Determine 1), there are almost 100 threat restrict tiers. These passive tier adjustments enhance the complexity of system administration and can lead to partial compelled liquidation, undermining customers’ pursuits.

We purpose to develop a nonlinear mannequin to simulate cheap place sizes for a given capital, enabling extra versatile and environment friendly threat administration. This method includes rebuilding the interior formulation system to attain self-consistency, offering a viable different to the present advanced threat restrict templates.

This paper proposes a brand new threat administration framework as a substitute for the present restrict fashions. The brand new method has already been carried out in KuCoin’s cross-margin system, exhibiting some apparent benefits:

1. It’s nearer to the place administration settings utilized by conventional exchanges, making it simpler for institutional capital to adapt.
2. It eliminates the necessity to regulate threat limits based mostly on place measurement or leverage utilization.
3. It simplifies operational processes, decreasing the burden on the alternate whereas mitigating the danger of harming customers’ pursuits to guard the alternate’s personal advantages.

This mannequin supplies a extra clear and streamlined method to threat administration, aligning each alternate operations and person pursuits.

The mannequin

Most Place Measurement

We assume {that a} person’s account holds capital C, and the value of the underlying asset’s futures contract is p. The preliminary margin fee r corresponds to the reciprocal of the leverage chosen by the person. Ignoring transaction charges, the variety of contracts the person can open is given by:

N = C/(p ∗ r)

Nonetheless, if the capital C is simply too massive or the margin fee r is simply too low, the related dangers for the alternate turn into important. Subsequently, when each C and rrr are mounted and C is massive, the utmost allowable place can be restricted by the alternate’s threat tiers to a lot lower than C/(p*r). Conversely, with smaller capital C, the place measurement can method C/(p*r).

Many exchanges implement dozens to lots of of threat tiers to handle this relationship. In consequence, customers incessantly want to regulate their tier degree as their capital grows. The target behind these restrictions will be roughly expressed utilizing a logarithmic operate:

N = ln(C/(p ∗ r) + 1)

Clearly, when C is massive, the primary spinoff of the logarithmic operate decreases, that means the achievable place measurement can be smaller than that calculated by a linear formulation. Nonetheless, this presents a problem: for the approximation ln(x+1)≈x to carry, C have to be small enough, and p have to be massive. In any other case, even with small C, customers should still be unable to attain the theoretical most place measurement of C/(p*r).

To handle this, we have to introduce a bigger scaling parameter okay based mostly on the traits of various contract sorts. The unique equation is then modified as follows:

N = okay ∗ ln(C/(p ∗ r ∗ okay) + 1)

This adjustment satisfies the wants of small-capital customers whereas additionally assembly the danger management necessities for large-capital customers.

To have in mind open positions and different margin necessities in KuCoin’s cross-margin system, let’s outline the next:

• F: Margin occupied by different contracts and open orders.
• E: Whole fairness within the person’s futures account.
• Q: Place measurement of pending orders aligned with the identical path as the brand new order.
• O: Present open place measurement (constructive if aligned with the brand new order, adverse if in the wrong way).

The equation for calculating the utmost allowable place is then:

N = max(0, okay ∗ ln((E − F )/(okay ∗ p ∗ r) + 1) − Q − O)

Subsequently, beneath this mannequin on KuCoin, for capital of a typical measurement, the connection between leverage and the utmost allowable place will be visualized as follows:

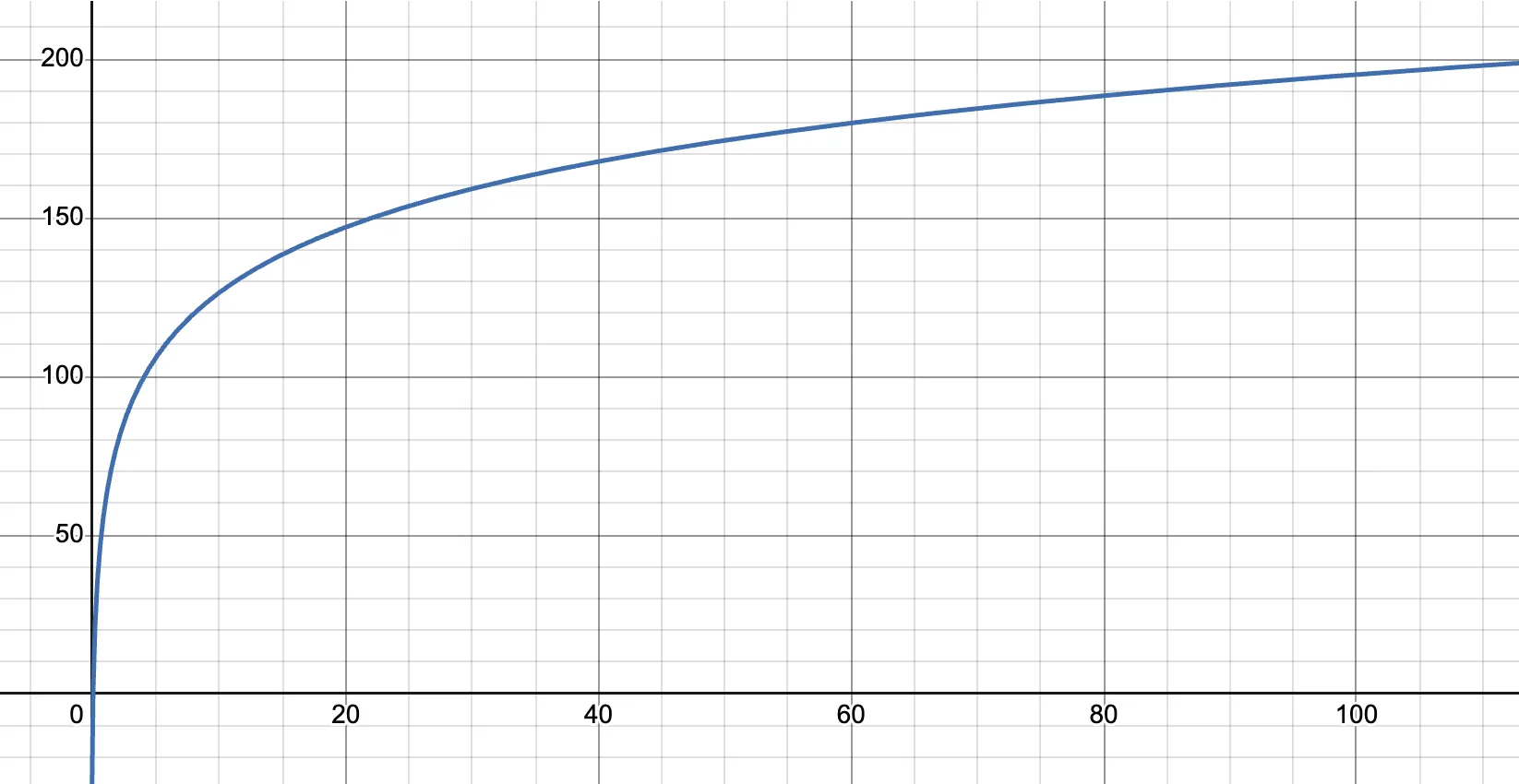
This chart displays how the mannequin ensures scalability and stability, balancing between the wants of smaller customers (to maximise place measurement) and threat management for bigger customers by means of nonlinear margin changes.

Nonetheless, on most exchanges (similar to OKX and Binance), the connection between leverage and place measurement usually follows a distorted curve:

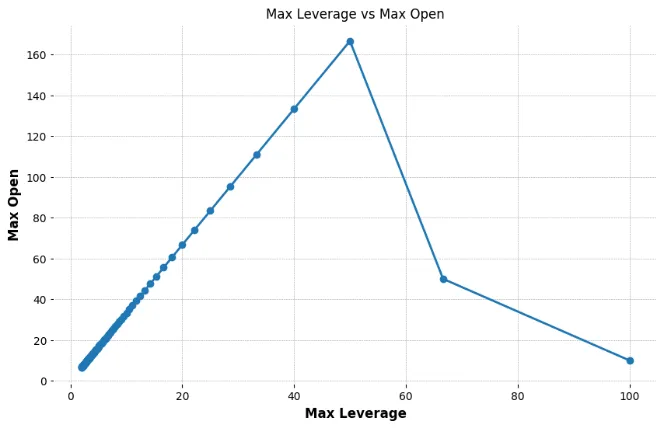
In truth, even MMR (Upkeep Margin Fee) follows an analogous sample. This may be notably difficult for large-capital customers. For instance, when the IMR (Preliminary Margin Fee) is ready at 50%, the MMR could be as excessive as 48%. In such instances, customers trying to open massive positions are restricted to utilizing low leverage, however the MMR is elevated to an unreasonable extent.

This setup limits customers’ means to successfully make the most of their capital, as leverage tiers shift abruptly and require frequent changes, decreasing flexibility. It creates an imbalance between threat administration and person expertise, making it troublesome for giant buyers to function effectively inside these constraints.

MMR and IMR

The MMR (Upkeep Margin Fee) basically serves as a compensation mechanism for the alternate to handle liquidation dangers. At its core, MMR displays the strain on liquidity extraction and desires to regulate dynamically with adjustments in open positions. Beneath, we derive the theoretical worth of MMR based mostly on liquidity-related metrics out there to the alternate.

Liquidity-Associated Variables

To correctly assess liquidity, the next variables are recognized, that are sometimes accessible to exchanges:

• μ: Pace of market order execution
• T: Time requirement for liquidation or buying and selling
• i: Worth/degree distance from the perfect bid or askj: Ticker time unit
• Qi: Common variety of orders at a distance iii from the order ebook
• S: Common measurement of an order (with SmS_mSm for market orders, SlS_lSl for restrict orders)
• N: Variety of orders (with Nm for market orders, Nc for cancellations, and Ni for restrict orders)

These values characterize the typical circumstances in a steady market.

Defining Person Place Metrics

• place: Instantaneous common place measurement of all customers, which might come from the alternate’s empirical values.
• pos: place measurement held by any person
• X: Sum of the traded quantity inside MMR ranges over the buying and selling interval
• MMRup: Higher restrict for MMR
• rMMR: Remaining worth of the MMR
• R: precise distance from greatest bid or ask, not the identical as r, usually depends upon i, j

Adjustment of MMR with Order Move

The pace of restrict order entries and cancellations is included as a part of the typical over a number of ranges. Provided that market orders usually tend to execute immediately, we have to account for this relative enhance or lower. The next relationships outline the dynamics:

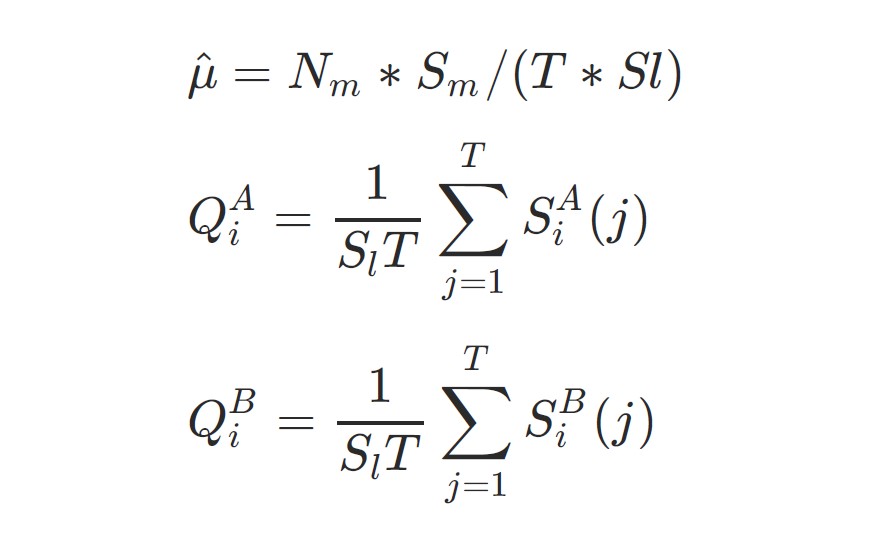
For instance, taking an extended place, the corresponding robust liquidation liquidity will be the purchase order amount (Q):

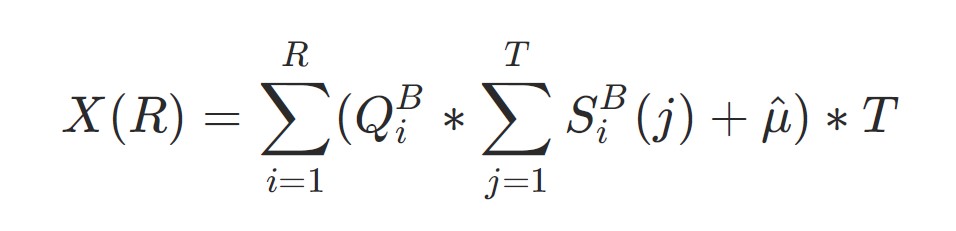
For alternate’s safety, we get:

X(R) = place R = f (place)
R = f (place)

Right here, it’s not far to succeed in that place and R have an roughly inverse relationship. And for minimal order amount:

R = p × MMR

The place is understood, given the constraint relationships of variables. MMR is impartial of p, so:

MMR = g(place) = z(Q, S, T , μ^, i, j) = f(place)/p

Subsequently, the ultimate worth of rMMR will be expressed as:

rMMR = min(MMRup, MMR)

From the above equations, it may be seen that, other than R, different variables similar to place, Q, S and T are all decided. Thus, R will be derived from these variables, and subsequently, MMR and rMMR will be calculated.

Moreover, the MMRup cap is critical as a result of the mannequin tends to be conservatively estimated, usually ignoring the constructive affect of key worth factors and key bid or ask ranges on the order ebook. Some research from CME (see Determine 2) illustrate this impact extra precisely.

The IMR (Preliminary Margin Fee) is often related to the leverage and liquidity of the underlying asset. Subsequently, it usually requires dynamic adjustment based mostly on elements similar to place measurement. It may be outlined as:

IMR = max(r, w(rMMR))

Right here, the IMR corresponds to the preliminary margin fee r talked about in Part 2.1. The operate w(rMMR) gives extra flexibility. For instance, if the alternate considers its liquidity to be steady, it will possibly apply a easy adjustment similar to: w(rMMR)=1.3×rMMR.

This method supplies a realistic technique to dynamically regulate margin charges, guaranteeing that the IMR displays present market circumstances and liquidity ranges. This makes the system extra adaptive in comparison with mounted margin guidelines, benefiting each customers and the alternate by means of efficient threat administration.

An approximate answer for okay

The parameter okay serves as a worldwide setting for every particular asset (image) and doesn’t have to account for current orders or open positions. In precept, the bigger the worth of okay, the extra positions a person can open. Nonetheless, there’s a vital constraint: the margin required for the utmost allowable place should not exceed the whole capital multiplied by the IMR.

To simplify, let’s assign the utmost allowable place formulation to a variable v:

v = okay ∗ ln(C/(p ∗ r ∗ okay) + 1)

The precise leverage have to be lower than or equal to the reciprocal of the utilized margin:

v/(C/p) <= 1/max(r, f (v, rMMR))

Let’s introduce a brand new variable y to interchange C (capital) and p (worth) for simplification:

y = C/p

we get:

v <= y/max(r, f (v, rMMR))

Besides for very small positions, 1.3 × rMMR (a simplified adjustment utilizing f(pos,rMMR) is usually lower than r. For smaller positions, the margin required turns into negligible, so such situations aren’t a priority for our threat mannequin. Equally, since MMRup units an higher restrict, it will also be ignored on this context.

Thus, we solely want to think about the smallest attainable worth for 1/IMR. The inequality can subsequently be simplified as:

v <= y/(1.3 ∗ f (place)/p)

This inequality demonstrates the connection between the utmost allowable place and precise leverage.

Not like different variables, place and R have a clearly outlined inverse relationship. Subsequently, the MMR derived from R can even have an inverse proportional relationship with place, and MMR will be expressed as follows:

MMR = para1 + para2/place

At this level, to imagine that the MMR beneath low positions aligns with the standard type (half of the inverse of leverage), the formulation will be written as:

MMR = 1/(2 ∗ maxleverage) ∗ (1 + pos/place)

Now we try to seek out the restrict of okay, then r in formulation (3) turns into 1/maxleverage.

And, substituting the variables, the inequality (18) can turn into:

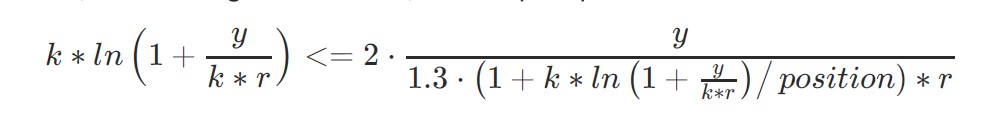
We observe that y (decided by the person’s capital) theoretically mustn’t have an effect on the worth of okay. Thus, okay is primarily depending on place. Though the minimal worth of okay varies with adjustments in y, the target is to establish the smallest attainable minimal throughout all circumstances. This ensures that the opening of positions stays protected beneath any state of affairs.

Right here, y/(okay*r) can nonetheless be substituted by a variable, however the equation stays advanced and troublesome to unravel analytically. Some intensive approximation experiments and iterative simulations reveal that okay converges to a quite simple expression(however the calculation of okay is a big endeavor, so it is not going to be elaborated on intimately right here):

okay <= e ∗ place

By adjusting the values of okay or place, we are able to obtain the impact that when the quantity of funds or the variety of open positions will not be massive, customers can confide in C/(p∗r). In any other case, they are going to be restricted. The dimensions of the amount and the diploma of limitation are each managed by okay and place. Subsequently, totally different cryptocurrencies usually correspond to totally different okay values.

The above is a quick introduction to KuCoin’s cross-margin threat restrict system. The benefits of this design and its user-friendliness are self-evident.

In KuCoin’s cross-margin system, other than threat limits, different components similar to threat ratios and order margin utilization are additionally dynamically managed utilizing the mark worth. This dynamic administration not solely maximizes the discharge of customers’ margin but additionally integrates seamlessly with the brand new threat restrict framework, enhancing system effectivity and person expertise.

determine 1:

determine 2:

1. “A Stochastic Mannequin for Order E-book Dynamics” by Rama Cont, Sasha Stoikov, and Rishi Talreja, Operations Analysis, Quantity 58, Subject 3, in 2010.
2. “Forecasting Preliminary Margin Necessities – A Mannequin Analysis” , Journal of Monetary Markets (Quantity 40, 2018)
3. Alfonsi, A., A. Schied, A. Schulz. 2010. Optimum execution methods in restrict order books with common form capabilities. Quant. Finance 10(2).